If by any chance Bell is wrong about his derivation of the inequalities it should be demonstrable using a computer simulation. This blog is an attempt to discuss the possibilities of such a model.
Spooky action at a distance
For long the discussion on the Bell inequalities as applicable on an EPR-Bohm like experiment has been going on. Today most physicists seem to accept the experimental results as being in favor of a non-local interpretation of the quantum mechanics phenomena of entanglement.
This contradicts the viewpoint of Einstein with his famous phrase on this subject as being some “Spooky action at a distance” fenomenon of nature.
No-Bell claims
In recently years some no-Bell claims have been made by different authors (1,2,3,4,7). Many of them give a violation for the Bell inequalities for a 22.5° angle between settings of Bob and Alice using a local realist calculation.
Event by event simulation
Being a probabilistic setup, one should be able to simulate the individual events of two particles hitting the polarizer’s or passing Stern-Gerlach apparatus and then being counted by detectors. The result of many repeats of this simulation should earn the typical bell shaped result, as has been documented for example by Dehlinger and Mitchell (5).
The model from De Raedt
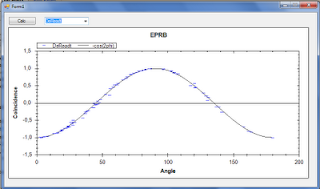
 |
| Result of the simulation from de Readt (6) |
De Raedt has published such a deterministic simulation in (6), which article includes a Fortan listing of the code used in their earliest models. I have checked their model by rewriting their program in an object oriented (OO) language (C#)¹. Their model does indeed produce the quantum results in a local realistic way. This is done by including the time-window in the simulation, which in real experiments is used to determine whether two click from the counters should be considered coming from the two pairs of entangled particles or not. Their model can be tested online at http://rugth30.phys.rug.nl/eprbdemo/simulation.php.
Critics however might oppose that when real experiments can be performed in such way that doubt about measured clicks being from entangled particle pairs can be excluded the model from de Raedt cannot be maintained.
The OO model
An object oriented language defines objects that mimics the properties and methods of real objects. In case of an EPR simulation, the filter object for example can have the property ‘rotation angle’, and the method ‘particleHit(Particle)’.
In the core of the EPR simulation initializes a particle (A) with its properties like a random polarization angle, and then creates its ‘entangled’ counterpart (B) based on the properties of (A). After the filters from Alice and Bob have also been initialized with random rotation angles, the particle A is subjected to the Alice’s filter’s ‘ParticleHit(Particle)’ function, and particle B to Bob’s.
In Alice’s filter there is no knowledge of the settings of Bob’s filter and vice versa.
The ‘ParticleHit’ function can only use local properties from the Particle and the filter itself, to determine whether a Boolean property from the Particle called ‘Absorbed’ is set to true or false.
The described process is repeated for example 10000 times, and each time the results are registered. The summary of these events should of course lead to the bell shaped curve showing the violation at 22.5° and 67.5°.
Hidden variables
While it might be tempting to start looking for hidden variables that corresponds to elements of reality, as is done by Bryan Sanctuary (9), to challenge the Bell inequalities with a local realistic model this is not strictly necessary. In de OO model the particles can be provided with any property, as long as it doesn’t contain information about the settings of the opposite polarizer. Also the ‘ParticleHit’ can be implemented at will (with the same condition applied).
Joy Christian for example has been publishing several articles (like 8) on violating the Bell inequalities in a local realistic way using Clifford algebra. If he is correct, including Clifford logic in this simulation should produce the expected results.
The code
Below the code for the model of de Raedt (6) is explained. The main loop is quite straightforward. The constants ‘d’, ‘tau’ and ‘k’ are used in the model from de Raedt (see (6) for a description). The full C# project can be found at https://sourceforge.net/projects/epr-bohm/ ².
PolarizationFilter PolarizationFilter1 = new
PolarizationFilter(NumberOfAnglesForStations, d, tau);
PolarizationFilter PolarizationFilter2 = new
PolarizationFilter(NumberOfAnglesForStations, d, tau);
// generate events
for (int i = 0; i < N * NumberOfAnglesForStations *
NumberOfAnglesForStations; i++)
{
//Initiate entangled particles
Crystal Cristal = new Crystal(Interpretation);
Particle Particle1 = Cristal.ParticleA;
Particle Particle2 = Cristal.ParticleB;
// pick an angle at station 1
int AngleIndexStation1 =
PolarizationFilter1.ChooseRandomAngleIndex();
// pick an angle at station 2
int AngleIndexStation2 =
PolarizationFilter2.ChooseRandomAngleIndex();
// hit station 1
PolarizationFilter1.ParticleHit(Particle1);
//station 2
PolarizationFilter2.ParticleHit(Particle2);
// count (model with time window)
if (Math.Abs(Particle1.DelayTime - Particle2.DelayTime) < k)
{
Ntiming[Particle1.Passed, Particle2.Passed, AngleIndexStation1,
AngleIndexStation2] += 1;
}
}
The simplest version of the particle object contains constructor logic and the two properties Polarization and Absorbed. The extra property ‘DelayTime’ is used in the de Raedt model:
public class Particle
{
public Particle()
{
this.Polarization = h.GetRandomTwoPiAngle();
}
public double Polarization
{
get;
set;
}
public bool Absorbed
{
get;
set;
}
public int Passed
{
get
{
if (this.Absorbed)
{
return 0;
}
return 1;
}
}
public double DelayTime
{
get;
set;
}
}
I use an object named ‘Crystal’ to initiate the two entangled particles. Notice that the constructer allows specifying different Calculations or ‘Interpretations’. Here only the calculation from DeRaedt is implemented:
public class Crystal
{
public Crystal(Calculation Interpretation)
{
ParticleA = new Particle();
ParticleB = new Particle();
Initialize(Interpretation);
}
private void Initialize(Calculation Interpretation)
{
switch (Interpretation)
{
case Calculation.DeReadt:
InitialiseDeRaedt();
return;
}
}
private void InitialiseDeRaedt()
{
// polarization of particle 2
ParticleB.Polarization = ParticleA.Polarization + h.PiOver2;
}
public Particle ParticleA { get; set; }
public Particle ParticleB { get; set; }
}
The polarizers are constructed with a list of randomly chosen angles. See above for the explanation of ‘d’ and ‘tau’.
public class PolarizationFilter
{
private double d;
private double tau;
public PolarizationFilter(int NumberOfAngles, int d, double tau)
{
InitiateAngles(NumberOfAngles);
this.d = d;
this.tau = tau;
}
private void InitiateAngles(int NumberOfAngles)
{
_Angles = new List<double>();
for (int ii = 0; ii < NumberOfAngles; ii++)
{
_Angles.Add(h.GetRandomPiAngle());
}
}
public int ChooseRandomAngleIndex()
{
_currentAngleIndex = GetRandomAngleIndex();
return _currentAngleIndex;
}
private int GetRandomAngleIndex()
{
// pick an angleIndex:
return (int)(((float)_Angles.Count) * h.GetRandom());
}
private int _currentAngleIndex = 0;
public List<double> Angles { get; set; }
public double Angle
{
get
{
return _Angles[_currentAngleIndex];
}
set
{
_Angles[_currentAngleIndex] = value;
}
}
public void ParticleHit(Particle Particle)
{
...
}
}
The method ‘particleHit’ again checks the Interpretation to be used and then executes the logic:
public void ParticleHit(Particle Particle)
{
switch (Calc_Epr.Interpretation)
{
case Calculation.DeReadt:
ParticleHitfromDeRaet(Particle);
break;
}
}
private void ParticleHitfromDeRaet(Particle Particle)
{
double malus = h.Malus(Particle.Polarization - this.Angle);
if (malus > h.GetRandomPlusMin())
{
Particle.Absorbed = true;
}
// delay time
Particle.DelayTime = Math.Ceiling(Math.Pow(Math.Pow((1 - malus
* malus),2), (d / 2)) * h.GetRandom() / tau);
}
As can be seen h provides some common functions. For instance, h.Malus(Angle) is implemented as:
public static double Malus(double Angle)
{
return Math.Cos(2 * Angle);
}
and h.GetRandomPlusMin()as:
public static Random r = new Random(DateTime.Now.Millisecond);
public static double GetRandomPlusMin()
{
return r.NextDouble()*2-1;
}
7. Event-by-Event Simulation of Quantum Phenomena: Application to Einstein-Podolosky-Rosen-Bohm Experiments, H. De Raedt, K. De Raedt, K. Michielsen, K. Keimpema, and S. Miyashita, Journal of Computational and Theoretical Nanoscience Vol.4, 957–991, 2007, http://rugth30.phys.rug.nl/pdf/jctn8.pdf
¹ While some might prefer a sequential code, the equivalence from the object in an OO language with the real objects that are simulated makes this environment very suitable for a hidden variable demonstration
² It can be tested by using the free Visual Studio express C# environment from http://www.microsoft.com/express/Downloads/#2010-Visual-CS.